Stack

Stack is a linear data structure that follows a particular order in which the operations are performed. The order may be LIFO(Last In First Out) or FILO(First In Last Out). LIFO implies that the element that is inserted last, comes out first and FILO implies that the element that is inserted first, comes out last.

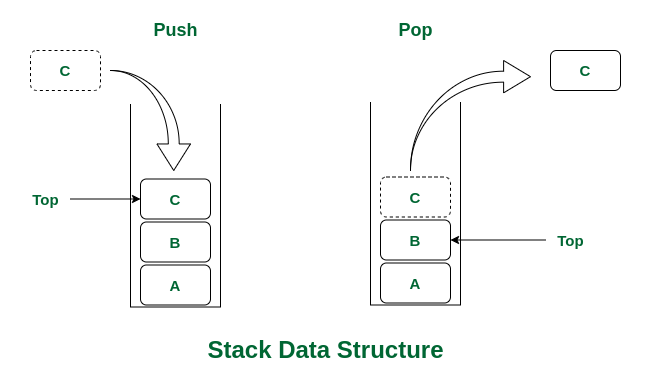
The stack data structure has many practical applications in computer science and programming, such as in memory management, function calls, and expression evaluation.

In memory management, the stack is used to store function calls, local variables, and other temporary data. As functions are called, they are pushed onto the stack, and as they return, they are popped off the stack, freeing up memory.

In programming, the stack can be used to evaluate expressions using postfix notation, also known as Reverse Polish Notation (RPN), where operands are pushed onto the stack, and operators are applied to the top two items on the stack.

The stack data structure is also used in web browsers to implement the back button functionality. Each time a user navigates to a new page, the page’s URL is added to the stack. When the user clicks the back button, the previous URL is popped off the stack, and the browser navigates back to that page. AI GENERATED

Basic operations:

In order to make manipulations in a stack, there are certain operations provided to us.

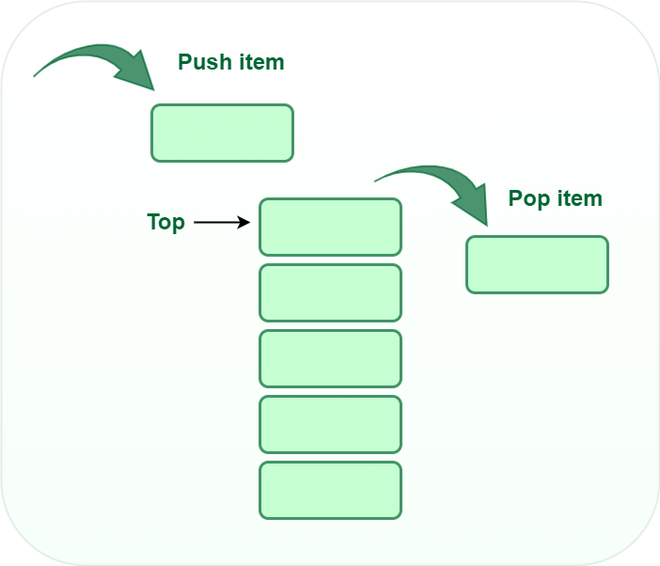
• push() to insert an element into the stack
• pop() to remove an element from the stack
• top() Returns the top element of the stack.
• isEmpty() returns true if stack is empty else false.
• size() returns the size of stack.

Types:

• Fixed Size Stack: As the name suggests, a fixed size stack has a fixed size and cannot grow or shrink dynamically. If the stack is full and an attempt is made to add an element to it, an overflow error occurs. If the stack is empty and an attempt is made to remove an element from it, an underflow error occurs.
• Dynamic Size Stack: A dynamic size stack can grow or shrink dynamically. When the stack is full, it automatically increases its size to accommodate the new element, and when the stack is empty, it decreases its size. This type of stack is implemented using a linked list, as it allows for easy resizing of the stack.

There are other types but i will present just these presented above. if you want to do know more about check this link

STRUCTURE:

A stack is a linear data structure in which the insertion of a new element and removal of an existing element takes place at the same end represented as the top of the stack.

To implement the stack, it is required to maintain the pointer to the top of the stack, which is the last element to be inserted because we can access the elements only on the top of the stack.

class Node<T>(element: T) {
    val value = element
    var next: Node<T>? = null
    var prev: Node<T>? = null
}

open class DoublyLinkedList<T> {
    protected var head: Node<T>? = null
    protected var tail: Node<T>? = null

    protected fun addMember(element: T) {
        val newElement = Node(element)
        if (head == null) {
            head = newElement
            tail = newElement
        } else {
            var current = head
            while (current?.next != null) {
                current = current.next
            }

            current?.prev = tail
            tail = newElement
            current?.next = tail
            tail?.prev = current
        }
    }

    fun traverse(action: (T) -> Unit) {
        var current = head
        while (current?.next != null) {
            current.value?.let(action)
            current = current.next
        }
        current?.value?.let(action)
    }
}

class Stack<T> : DoublyLinkedList<T>() {

    fun push(element: T) {
        addMember(element)
    }

    fun top() = this.tail

    fun pop() {
        val current = tail?.prev
        current?.next = null
        tail = current
    }

    fun size(): Int {
        var count = 0
        this.traverse { count++ }
        return count
    }
}

fun main() {
    val stack = Stack<Int>()
    for (i in 1..8) {
        stack.push(i)
    }
    println("Showing the stack:")
    stack.traverse { value ->
        print("$value,")
    }
    println("Show the top before pop: ${stack.top()?.value} size: ${stack.size()}")
    stack.pop()
    println("Show the top after pop: ${stack.top()?.value} size: ${stack.size()}")
    stack.traverse {
        print("$it,")
    }
}

REFERENCES:

https://www.geeksforgeeks.org/stack-data-structure/
https://www.tutorialspoint.com/what-is-postfix-notation https://www.geeksforgeeks.org/introduction-to-stack-data-structure-and-algorithm-tutorials/