Heap
Heap is a Data Structure based on Tree, specifically in the complete-binary-tree. Basically a completly binary tree is a tree where all levels are filled completeely except the lowest level nodes which are filled from as left as possible.

One real-life analogy for a heap data structure could be a priority queue at an amusement park. When you’re waiting in line for a ride, you’re essentially in a queue, and the order in which you get to ride the ride is determined by your position in the queue. However, sometimes certain people are given priority based on certain factors, such as being disabled or having a fast pass.
A heap data structure works in a similar way, but instead of a queue for people waiting in line, it’s a data structure for storing and retrieving items based on their priority. In a heap, items are stored in a way that ensures that the highest priority item is always at the top, so it can be retrieved quickly.
Different of BST (binary search tree) heap has the root value (the value from the root node) as the largest value, i.e the root node will contain the more valuable element in the tree. So it means that an complete-binary-tree can pass by the proccess of “Heapify”.
check some properties of it that differs from complete-binary-tree:
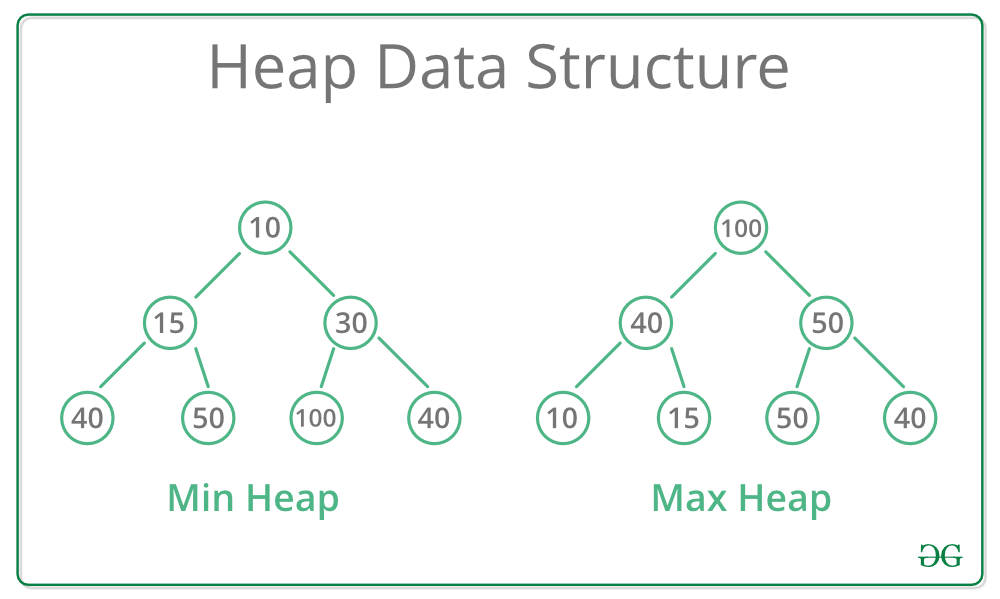
- always greater than its child node/s and the key of the root node is the largest among all other nodes. This property is also called max heap property.
- always smaller than the child node/s and the key of the root node is the smallest among all other nodes. This property is also called min heap property.
Types:
Generally, Heaps can be of two types:
- Max-Heap: In a Max-Heap the key present at the root node must be greatest among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.
- Min-Heap: In a Min-Heap the key present at the root node must be minimum among the keys present at all of it’s children. The same property must be recursively true for all sub-trees in that Binary Tree.
Basic Operations:
- Heapify: a process of creating a heap from an array.
- Insertion: process to insert an element in existing heap time complexity O(log N).
- Deletion: deleting the top element of the heap or the highest priority element, and then organizing the heap and returning the element with time complexity O(log N).
- Peek: to check or find the most prior element in the heap, (max or min element for max and min heap).
Structure:
package datastructures.heap
import kotlin.math.log2
import kotlin.math.pow
class Heap<T : Comparable<T>> {
private val items = mutableListOf<T>()
private val size : Int
get() = items.size
fun heapify(array: Array<T>) {
items.clear()
items.addAll(array)
for (i in (items.size / 2) downTo 0) {
heapifyDown(i)
}
}
fun insert(item: T) {
items.add(item)
heapifyUp(items.lastIndex)
}
fun delete(): T? {
if (items.isEmpty()) {
return null
}
val item = items[0]
items[0] = items.last()
items.removeLast()
heapifyDown(0)
return item
}
fun peek(): T? {
return items.firstOrNull()
}
private fun heapifyUp(index: Int) {
var currentIndex = index
var parentIndex = (currentIndex - 1) / 2
while (parentIndex >= 0 && items[parentIndex] < items[currentIndex]) {
swap(parentIndex, currentIndex)
currentIndex = parentIndex
parentIndex = (currentIndex - 1) / 2
}
}
private fun heapifyDown(index: Int) {
var currentIndex = index
var leftChildIndex = 2 * currentIndex + 1
var rightChildIndex = 2 * currentIndex + 2
var maxChildIndex = currentIndex
if (leftChildIndex < items.size && items[leftChildIndex] > items[maxChildIndex]) {
maxChildIndex = leftChildIndex
}
if (rightChildIndex < items.size && items[rightChildIndex] > items[maxChildIndex]) {
maxChildIndex = rightChildIndex
}
if (maxChildIndex != currentIndex) {
swap(currentIndex, maxChildIndex)
heapifyDown(maxChildIndex)
}
}
private fun swap(i: Int, j: Int) {
val temp = items[i]
items[i] = items[j]
items[j] = temp
}
fun printHeap() {
val height = log2(size.toDouble()).toInt() + 1
val maxLevelNodes = 2.toDouble().pow(height - 1).toInt()
val nodeWidth = peek().toString().length + 2
var nodeCount = 0
for (i in 1..height) {
val levelNodes = 2.toDouble().pow(i - 1).toInt()
val leftPadding = (maxLevelNodes - levelNodes) * nodeWidth / 2
for (j in 1..levelNodes) {
val node = if (nodeCount < size) getNode(nodeCount++) else ""
print(" ".repeat(leftPadding))
print(node.padStart(nodeWidth, ' '))
}
println()
}
}
private fun getNode(index: Int): String {
return if (index < size) items[index].toString() else ""
}
}
fun main() {
val maxHeap = Heap<Int>()
maxHeap.heapify(arrayOf(4, 1, 3, 2, 16, 9, 10, 14, 8, 7))
println("Max heap:")
println("Peek: ${maxHeap.peek()}") // 16
println("Delete: ${maxHeap.delete()}") // 16
println("Peek: ${maxHeap.peek()}") // 14
maxHeap.insert(20)
println("Peek: ${maxHeap.peek()}") // 20
val minHeap = Heap<Int>()
minHeap.heapify(arrayOf(4, 1, 3, 2, 16, 9, 10, 14, 8, 7))
println("Min heap:")
println("Peek: ${minHeap.peek()}") // 1
println("Delete: ${minHeap.delete()}") // 1
println("Peek: ${minHeap.peek()}") // 2
minHeap.insert(0)
println("Peek: ${minHeap.peek()}") // 0
minHeap.printHeap()
}
For what it’s?
Operating Systems: A heap can be used in operating systems to manage processes running on a computer. The operating system can assign a priority level to each process, and use a heap to efficiently schedule processes in order of priority.
Dijkstra’s Algorithm: Dijkstra’s algorithm is a popular shortest path algorithm used in computer science. A heap data structure can be used to efficiently retrieve the next closest node during the algorithm’s traversal of a graph.
Event-driven Simulations: In event-driven simulations, events are added to a priority queue based on their timestamp. A heap can be used to manage this priority queue, ensuring that the events are processed in the correct order.
Huffman Coding: Huffman coding is a data compression algorithm that uses a binary heap to construct a Huffman tree. The tree is then used to assign variable-length codes to each symbol in the input data, resulting in a compressed representation of the original data.
Network Routing: A heap can be used to implement Dijkstra’s algorithm for network routing, where each node in the network represents a point of communication and the edges represent communication channels between nodes. The heap can be used to determine the next best node to route a message through, based on factors such as distance and network congestion
REFERENCES:
https://en.wikipedia.org/wiki/Heap_(data_structure)
https://www.geeksforgeeks.org/heap-data-structure/