Tree
A tree data structure is a hierarchical structure that is used to represent and organize data in a way that is easy to navigate and search. It is a collection of nodes that are connected by edges and has a hierarchical relationship between the nodes. The topmost node of the tree is called the root, and the nodes below it are called the child nodes. Each node can have multiple child nodes, and these child nodes can also have their own child nodes, forming a recursive structure.
This data structure is a specialized method to organize and store data in the computer to be used more effectively. It consists of a central node, structural nodes, and sub-nodes, which are connected via edges. We can also say that tree data structure has roots, branches, and leaves connected with one another.
Types:
- Binary Tree
- Binary Search Tree
- AVL Tree
- B-Tree
Terminologies In Tree Data Structure:
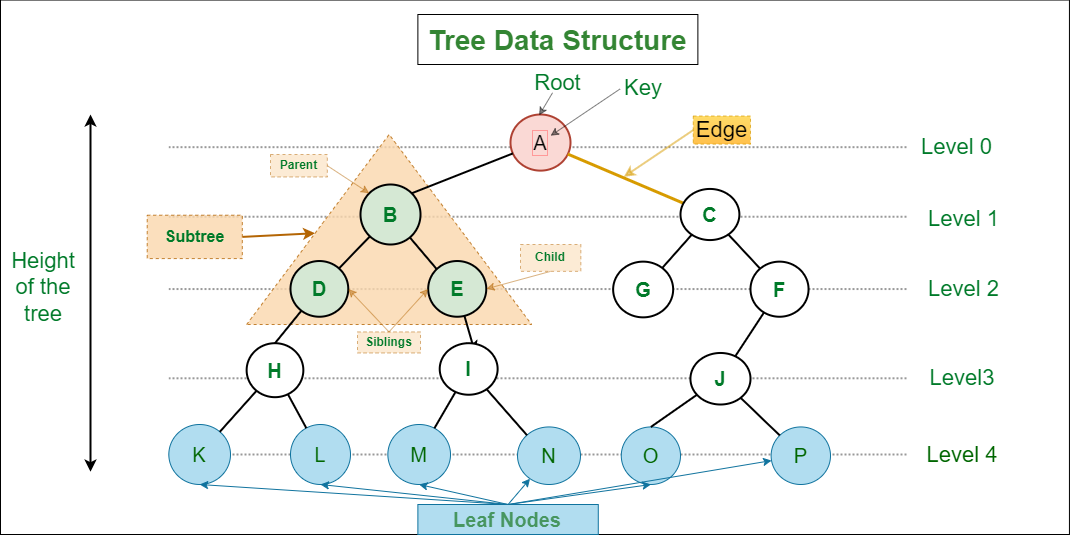
Parent Node: The node which is a predecessor of a node is called the parent node of that node. {B} is the parent node of {D, E}.
Child Node: The node which is the immediate successor of a node is called the child node of that node. Examples: {D, E} are the child nodes of {B}.
Root Node: The topmost node of a tree or the node which does not have any parent node is called the root node. {A} is the root node of the tree. A non-empty tree must contain exactly one root node and exactly one path from the root to all other nodes of the tree. Leaf Node or External Node: The nodes which do not have any child nodes are called leaf nodes. {K, L, M, N, O, P} are the leaf nodes of the tree. Ancestor of a Node: Any predecessor nodes on the path of the root to that node are called Ancestors of that node. {A,B} are the ancestor nodes of the node {E}
Descendant: Any successor node on the path from the leaf node to that node. {E,I} are the descendants of the node {B}.
Sibling: Children of the same parent node are called siblings. {D,E} are called siblings. Level of a node: The count of edges on the path from the root node to that node. The root node has level 0. Internal node: A node with at least one child is called Internal Node. Neighbour of a Node: Parent or child nodes of that node are called neighbors of that node.
Subtree: Any node of the tree along with its descendant.
Properties of a Tree:
Number of edges: An edge can be defined as the connection between two nodes. If a tree has N nodes then it will have (N-1) edges. There is only one path from each node to any other node of the tree.
Depth of a node: The depth of a node is defined as the length of the path from the root to that node. Each edge adds 1 unit of length to the path. So, it can also be defined as the number of edges in the path from the root of the tree to the node.
Height of a node: The height of a node can be defined as the length of the longest path from the node to a leaf node of the tree. Height of the Tree: The height of a tree is the length of the longest path from the root of the tree to a leaf node of the tree.
Degree of a Node: The total count of subtrees attached to that node is called the degree of the node. The degree of a leaf node must be 0. The degree of a tree is the maximum degree of a node among all the nodes in the tree. Some more properties are:
Traversing in a tree is done by depth first search and breadth first search algorithm. It has no loop and no circuit It has no self-loop Its hierarchical model.
Basic Operation:
- Create – create a tree in data structure.
- Insert − Inserts data in a tree.
- Search − Searches specific data in a tree to check it is present or not.
- Preorder Traversal – perform Traveling a tree in a pre-order manner in data structure .
- In order Traversal – perform Traveling a tree in an in-order manner.
- Post order Traversal –perform Traveling a tree in a post-order manner.
Structure:
In this section i will structure just the Binary Tree, for the other ones i suggest you to create one by yourself.
package datastructures.tree
import java.util.*
class Node<T>(var value: T) {
var left: Node<T>? = null
var right: Node<T>? = null
}
class BinaryTree<T: Comparable<T>> {
var root: Node<T>? = null
fun insert(value: T) {
root = insertRecursive(root, value)
}
private fun insertRecursive(node: Node<T>?, value: T): Node<T> {
if (node == null) {
return Node(value)
}
if (value < node.value) {
node.left = insertRecursive(node.left, value)
} else if (value > node.value) {
node.right = insertRecursive(node.right, value)
}
return node
}
fun search(value: T): Boolean {
return searchRecursive(root, value)
}
private fun searchRecursive(node: Node<T>?, value: T): Boolean {
if (node == null) {
return false
}
if (value == node.value) {
return true
}
return if (value < node.value) {
searchRecursive(node.left, value)
} else {
searchRecursive(node.right, value)
}
}
fun preorderTraversal(): List<T> {
val result = mutableListOf<T>()
preorderTraversalRecursive(root, result)
return result
}
private fun preorderTraversalRecursive(node: Node<T>?, result: MutableList<T>) {
if (node != null) {
result.add(node.value)
preorderTraversalRecursive(node.left, result)
preorderTraversalRecursive(node.right, result)
}
}
fun inorderTraversal(): List<T> {
val result = mutableListOf<T>()
inorderTraversalRecursive(root, result)
return result
}
private fun inorderTraversalRecursive(node: Node<T>?, result: MutableList<T>) {
if (node != null) {
inorderTraversalRecursive(node.left, result)
result.add(node.value)
inorderTraversalRecursive(node.right, result)
}
}
fun postorderTraversal(): List<T> {
val result = mutableListOf<T>()
postorderTraversalRecursive(root, result)
return result
}
private fun postorderTraversalRecursive(node: Node<T>?, result: MutableList<T>) {
if (node != null) {
postorderTraversalRecursive(node.left, result)
postorderTraversalRecursive(node.right, result)
result.add(node.value)
}
}
fun printTree() {
val root = root ?: return
val maxLevel = maxLevel(root)
printNode(Collections.singletonList(root), 1, maxLevel)
}
private fun printNode(nodes: List<Node<T>?>, level: Int, maxLevel: Int) {
if (nodes.isEmpty() || nodes.all { it == null }) {
return
}
val floor = maxLevel - level
val edgeLines = Math.pow(2.0, Math.max(floor - 1, 0).toDouble()).toInt()
val firstSpaces = Math.pow(2.0, floor.toDouble()).toInt() - 1
val betweenSpaces = Math.pow(2.0, floor + 1.toDouble()).toInt() - 1
printWhitespaces(firstSpaces)
val newNodes = mutableListOf<Node<T>?>()
for (node in nodes) {
if (node != null) {
print(node.value)
newNodes.add(node.left)
newNodes.add(node.right)
} else {
newNodes.add(null)
newNodes.add(null)
print(" ")
}
printWhitespaces(betweenSpaces)
}
println()
for (i in 1..edgeLines) {
for (node in nodes) {
printWhitespaces(firstSpaces - i)
if (node == null) {
printWhitespaces(edgeLines + edgeLines + i + 1)
continue
}
if (node.left != null) {
print("/")
} else {
printWhitespaces(1)
}
printWhitespaces(i + i - 1)
if (node.right != null) {
print("\\")
} else {
printWhitespaces(1)
}
printWhitespaces(edgeLines + edgeLines - i)
}
println()
}
printNode(newNodes, level + 1, maxLevel)
}
private fun printWhitespaces(count: Int) {
for (i in 0 until count) {
print(" ")
}
}
private fun maxLevel(node: Node<T>?): Int {
return if (node == null) {
0
} else {
maxOf(maxLevel(node.left), maxLevel(node.right)) + 1
}
}
}
fun main() {
val tree = BinaryTree<String>()
tree.insert("apple")
tree.insert("banana")
tree.insert("apoja")
tree.insert("cherry")
tree.insert("date")
tree.printTree()
}
For what it’s?
Trees are commonly used to represent or manipulate hierarchical data in applications such as:
File systems for: Directory structure used to organize subdirectories and files (symbolic links create non-tree graphs, as do multiple hard links to the same file or directory) The mechanism used to allocate and link blocks of data on the storage device Class hierarchy or “inheritance tree” showing the relationships among classes in object-oriented programming; multiple inheritance produces non-tree graphs Abstract syntax trees for computer languages
Natural language processing: Parse trees Modeling utterances in a generative grammar Dialogue tree for generating conversations Document Object Models (“DOM tree”) of XML and HTML documents Search trees store data in a way that makes an efficient search algorithm possible via tree traversal A binary search tree is a type of binary tree Representing sorted lists of data
Computer-generated imagery: Space partitioning, including binary space partitioning Digital compositing Storing Barnes–Hut trees used to simulate galaxies Implementing heaps Nested set collections Hierarchical taxonomies such as the Dewey Decimal Classification with sections of increasing specificity. Hierarchical temporal memory Genetic programming Hierarchical clustering
REFERENCES:
https://www.geeksforgeeks.org/introduction-to-tree-data-structure-and-algorithm-tutorials/ https://en.wikipedia.org/wiki/Tree_(data_structure)